原文轉載自:Gamasutra(Water Interaction Model For Boats in Video Games)
原作者:Jacques Kerner於 2015年2月27日
以下文章內容,除經另行註明,係由Gamasutra社群的成員所著。
其中表達的想法與意見為該作者所有,並不代表Gamasutra以及其母公司。
Jacques Kerner是Avalanche Studios的資深軟體工程師。(編註:知名系列作是Just Cause)
讓我們談談載具物理吧!
我們在電玩遊戲中關於載具物理的事談論得還不夠多。網路上關於電玩遊戲載具物理的文章少如稀星,而且通常是在說要怎麼入門。現今的電玩遊戲載具工程師會發現自己身處在相對來說是真空的環境之中。或是因為這似乎太難去解釋了,亦或是相較於"正確的"真實模擬來說,我們羞於自己使用偷吃步、簡化、和抄捷徑的方法。不管理由是什麼,電玩遊戲在模擬載具時有著獨特的限制性,而這件事因此有下筆的價值。這個引人入勝的話題參雜了不只物理學、鏡頭功夫、聲音、特效、還有人類的感知甚或是心理學。
我選擇從船隻開始說起是因為,嗯,我最近就在做船的東西,但同時也因為我發現它們的動力學就算以做研究的等級來看也還沒有被完全瞭解透徹(雖然大部份都已被破解了)。正因如此,制定船隻模型和理論的方式讓它很難被直接應用在電玩遊戲中。或是它們會需要非常昂貴的方法來進行模擬,基本上來說是不可能隨時掌控並應對設計師和玩家千變萬化的需求。但要寫出一個能捉到船隻關鍵特性的簡化版模型是有可能的。這其中絕對包含著藝術成份、也牽涉到驚險的放手一搏、以及一部份可能會讓某位Kelvin或Stokes在他們墳裡打滾抓狂的創意物理學。(編註:Kelvin-Stoke Theorem 克耳文-斯托克斯定理、旋度定理)
船隻物理學系列
在這個系列中我展示了一個演算法,用來計算對水中船隻來說最重要的作用力。最主要的動機是開發一個能夠捕捉到水中船隻主要動力學特性的模型,同時要避免訴諸於複雜且昂貴的流體學力學演算。
我限制自己要在合理的效能預算中做出來,也就是每艘船要少於1ms。這模型必須要夠穩固,以模擬形狀和尺吋多變的船隻從平靜水域到狂風暴雨中的行為演變。
這個系列文的第一篇會處理關於靜水的力,但也會為了計算這個模型中所有其他的力而先打好重要基底。其他的力是那些因為船隻和水互相連動所造成的動態的力。它們會在之後的文章中加以討論。
第一次學浮力就上手
在我跳入演算法之前,我想要複習一下浮力。我們所要做的是計算部份沉體所受的浮力大小和施力點。
當一個物體有部份沉入了流體之中,這流體就會基於本身的壓力來對物體的表面施力。壓力越大,施力越大。力是流體中許多水粒子在移動時碰撞到物體表面彈性表現的產物,就像是完美的撞球那樣。這是很微小的力,這個作用就算是水沒有往特地方向流動(水流)或是船隻靜止不動時也能夠感受到,而也因此它被稱為靜壓力。這些所有原子或分子碰撞表面的淨力會和表面垂直。另一個要留意的是水中的壓力會隨著深度而增加(只在有重力的星球會如此),因為越深的地方代表著有越來越多的水在以自身的重量往下壓。然而,壓力本身沒有特定的方向性,而且就算是在水中的某一個點上沒有流體的存在,這個點的壓力仍然會和整體的深度有關聯。(註一)
靜壓力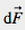 在一個小型平面的區域
在一個小型平面的區域 上之作用表現定義如下:
上之作用表現定義如下:
隨著深度而增加的力量對浮力來說是非常重要的,因為總浮力是物體表面在垂直方向上所受到的靜壓力不平衡所致。靜壓力在水平方向的分力會全部被抵消。直覺來看,這是因為容積(封閉的)中的每一個微小的面上,你永遠都可以找到另一個在反方向且位於同深度的面。因為靜壓力的大小是相同的,但卻作用在不同的方向,所以他們抵消了。另一方面,垂直方向的分力不會完全抵消。整體來說,因為容積是封閉的,法線指向下方的面對比法線指向上方的面一般會在較深的地方。所以,法線指向下的面的壓力獲勝。壓力是法線的反方向,所以合力會指向上,如此所示[2]合力的大小會等同於"被移開的流體",也就是注滿了水的物體容積的重量。(編註:簡單來說就是阿基米德原理的"被排開的水的重量等同浮力")
萬事俱備,只欠東風:在處理浮力的所有準備事項中,我們還需要靜壓力的施力點。浮力的施力點和所有靜壓力矩抵消的那個點有關。如果我們繼續去驗證沉體上的各個小部份基礎面,事情會變得不是那麼顯而易見。因為靜壓力會隨著深度變大,靜壓力在特定非水平面上的施力點一般來說會低於面的中心。如附件A(文章最底)所示,這個三角形沉體上——這對遊戲來說特別有用,因為我們傾向將所有東西都三角形化——施力點永遠都會比中心還來得低。然而不知何故,這些一般來說會施力在任一個面中心下方的所有力矩總合仍然會在容積的質心附近抵消。正式的證明可以在應用高—奧公式(Ostrogradsky-Gauss theorem)又稱為散度定理(divergence theorem)[2]中找到。這也可以用數字來驗證。我會提到這個的原因是,如果你想將物體拆解成許多的面,就用三角形吧,並將它們的所有靜壓力和力矩加總起來,你可能會想要去簡化力矩的計算,假定每個三角形的基本力作用在中心點上(更容易去處理)。然而若你如此做,你不會得到正確的結果。你會算出正確大小的力,但是你在沉體的中心附近會有多出來的力矩,而船可能會倒向一邊就此長眠,就算是在完全平坦的水面上也是如此。當你為了要節省效能而使用低多邊形數的網格(Mesh)時就會格外明顯,因為每一個三角形的錯誤會變得相對重大。另一方面,如果你用許多小三角形,這個簡化造成的錯誤便會大幅度減緩,而這樣的簡化也會變得可以接受。但在正確的中心做出複雜的計算和船殼上的三角形數量之間需要做個取捨。附件A指出了三角形沉體上靜壓力的施力點位置公式。
翻船的兩個方法
按照我們剛才所複習的,有兩種方式可以計算浮力。容積法:估算沉入流體中的容積並決定質心。表面法:判斷沉入流體中的表面並計算施在面上的力。這兩個方法如果應用得當的話應該會有相同的結果。
在不過份追求容積法和表面法近似值的情況下,兩者都需要我們判斷船殼和水的交會之處。這可能會使人惱羞,特別是當你要考量非平整的水平面時:這聽起來既昂貴又複雜。這或許是為何使用簡易的容積基本元件會讓這麼多人心動的原因。舉例來說,球形:對比上使用複雜的形狀來和水面交叉,計算球形沉入水中的容積又快又簡單,前題是水面在其周圍時近似於平面。這甚至可以用解析法來做判斷,也就是,至少以理論來說,這就是無限精準,或是和浮點運算所允許的準度一樣(沒錯,本文就是有這麼多雙關語)。也可以看成物體在水上載浮載沉時沉入的容積會不斷且逐漸改變,而遊戲中常常需要物理模組的連續性。但利用球形來逼近(Approximating)典形的船殼可能會很快地變成一場惡夢,因為這會需要許多不同大小的球形。由於球形是緻密堆積時最爛的選擇,你會在球與球之間留下很顯眼的空隙(圖一)。球形在容積中的緻密堆積有其上限,就算是利用不同半徑的球形也是一樣[5]。這些空隙的存在會帶來很顯著的不規則浮力。球形也可以做成可重疊的,但如此一來沉入的容積就會被高估了。最後呢,雖然要計算平面和球形的交叉是很簡單的,要計算球形和隨意亂動的水平面可費工多了,而我們同時可能還要找到一個能讓船殼和水交會的方法。
| 圖一:用球形來逼近船的容積並不可行。 |
物體的容積也可以像素化,舉例來說,用一堆像是方塊的容積基本元件來做逼近。和水交會到的像素可以再進一步像素化,直到符合某種程度的精確度。容積逼近法的麻煩之處在於它們解答(有些粗略)的問題是"有多少的水被排開了?",但對於判定物件沉入水中的吃水線可說是毫無用處,而這對於像是水花和泡沫這些水的特效,或是判定接觸到水的表面形狀為何等很有用處,除非說你使用了數量多到噁心的像素。
假設我們可以精確計算沉入水中的船殼之表面,我們仍然要在容積法和表面法之間做出選擇。用容積法的話,我們必須要將沉入的船殼表面給封閉起來形成封閉容積,計算它的總容積和質心,並且於該處施以浮力。用表面法的話,我們要計算每一個潛入水中的表面元素(三角形)靜壓力,然後加總物件中心附近重力的線衝量和角衝量。
表面法的優點是它不需要將容積封閉,所有的東西都已經做好直接將力加總的準備了。容積法的話,潛入的容積包含的可能不只一個容積。舉例來說,在雙體船上很容易看到這種狀況。但縱使船上沒有任何的洞,這代表和水的交會可能有兩個或更多的容積要封閉起來,而我們可能需要判斷哪一個沉入的三角形對哪一個容積有關係,也就是這個方法具有額外的複雜程度。表面法在這方面更為好用,因為它運用起來不用理形成的容積形狀數量,而且不需要封閉。它就是我用來做演算法的方法。
演算法的結構
我現在要開始概述演算法的結構,還有幾個關鍵的簡化讓它能運行地更快同時產出適當的結果。
我做的第一個假設是水面會以像是三角形網格的東西來表現,三角形的頂點會和水流動時的影格一起動作。這方法當然不適用於所有狀況,但是要用三角類型的網格來模擬水面一直都很可行的。在本文的後段我會描述要如何在水面上做抽樣,並準備一個能夠表現物體周圍水面的三角形網格。
主要的目標是要判斷水面和船殼面的交會。在看了Edouard Halbert [1]的實作之後,我開始著手實作一個能將所有水面和三角形交會的可能性都納入考量的精確解法。這個題目有些複雜,因為理論上一個平面要將三角形分割的方式有一大堆。一個水面可以從許多地方切開三角形,從中間穿越且不碰到任何邊線,或是將所有的頂點都淹過去。每個被淹過的區域都需要被三角形化,但這些區域並不必然為凸狀,導致三角形化變得更難(且變更慢)。此外,這些狀況相對來說都很常見。就算是在相對平靜的水面上這些狀況也會很快就發生,並且需要以某種方式妥善地處理,被淹過的表面在數量上才不會造成不真實的不連續感。在花了點時間實裝完美精準但效能非常緩慢的交叉演算法後,我發現我需要找出方法來簡化演算法同時不能犠牲掉太多的一般行為。我在此展示的演算法是這些簡化後的產物。我不會秀出第一版精準演算法的細節,因為那十分地冗長無趣,而且最終優化演算法的版本運作情況很好,速度也突飛猛進。
優化後演算法的結構如下:漂浮的物體是用三角形網格,也就是船殼來做逼近的。我會判定船殼上每個頂點距離水面上的高度。若距離水面上的高度為負的,那頂點就是位於水下。三個頂點都在水面上的三角形會被視為完全離開水面。這就是一種簡化,因為實際上水可能會高過三角形的某部份卻低於全部三個頂點,如圖四所示。同樣地,若三個頂點都低於水面的話我們就將其視為完全沉體,儘管實際上水可能會低於三角形的某部份也是一樣。當只有一或二個頂點低於水面時,我會將三角形拆成一個低於水面的區域和一個高於水面的區域,如同圖二所示。若低於水面的區域不是三角形的話,我會更進一步去將之三角形化。我大膽(而且在理論上也是不正確)地假設水面在沉沒的頂點和未沉入的頂點之間只會切過一個邊。圖三秀出一些不準確的交會例子。最終我會有一大堆的三角形,這些三角形都是在水面底下的。我接著會計算運作在這些三角形上的靜壓力和動壓力。
| 圖二:四個三角形和水塊交會的簡化範例。由左至右來看,三角形分別有0, 1, 2, 3個頂點沉入水中。兩個頂點沉入時我們需要更進一步地將沉入的部份三角形化。請注意到和水的交會在此並不準確。這是因為之後會解釋的另一項簡化結果。 |
| 圖三:這裡有三個優化演算法不夠周全的案例。紅色的區域表示應視為在水底下的三角形,但卻被忽略了。在左方的兩個三角形和水有交叉,但兩者都沒有頂點是在水底下的。在中間的三角形是以透視法所看到的,它的邊線甚至和水面都沒有交叉,水的波峰直接打穿三角形的中間。在右方的三角形有兩個頂點在水底下,但水面還是從這兩個頂點之間的邊線離開了三角形。 |
| 圖四:這是一個水面起伏較大的案例。船殼右下方較大型的三角形和許多不同的區塊交會,其中一個區塊沒有和任何的邊線有交會。更糟的是,這個區域可能是個曲面,讓三角形化沒辦法那麼快速。為了要應付所有類似這樣的狀況會耗費開發時間和執行效能。最終,在所有嚴謹的考量下,水面會因為船的存在而變動,而使得以上的狀況變得沒有意義。 |
對一個船模組來說,這些狀況都沒有它看起來得那麼重要。犠牲精確度在實例上並不是一個什麼太大的問題,只要船殼的三角形相較於我們所關切到最小水波的振幅和波長來說不要太大就好了。
我提出的這個方法最主要的好處就是一開始就可以處理所有的頂點,先不用管是哪三個組成一個三角形。所有的資訊接著可被用在處理每一個三角形,導出沉入水裡的有0個,1個,或2個的三角形。三角形交會的部份處理起來簡單又快速。大多數的處理若需要的話可以適用平行法來搞定。我們同時也可以知道沉沒的三角形數量最大值為何:也就是船殼三角形數量的兩倍。這讓我們可以用個簡單的陣列來預先分配所有的記憶體。
在下一個部份,我會展示實裝時的重要細節,像是要如何去逼近水面使檢查水深最有效率、如何去切割只有一或兩個頂點在水裡的三角形、以及如何計算浮力。
實裝的細節
水塊
為了要判定每個頂點距離水面的高度,我們需要一個快速的方法來決定某一處下方水的所在位置。在特定的遊戲或模擬中有很大一部份是要仰賴水是以什麼方式被模擬的。若水面是平的或僅以簡單的功能來做描述的話,那只要在每次詢問時很單純地直接取樣或計算就可以快速決定距離水面的高度。而另一種利用演算法來判斷距離水面高度的方法,花費不只高昂而且在查詢時還有限制數量。這個方法就是舉例來說像是Tessendorf波這樣,以快速傅立葉轉換為基底的的手法[4]。在這種案例中,我建議在物件周圍一次性地對距離相等的點做採樣,以此創造出一份可以在之後用來做高度查詢的高度圖(Height Map)。我會用水塊來代指這張圖。這水塊必須至少和這個物件的垂直投影一樣大。舉例來說,你可以從一個邊長和物件方塊對角線一樣長的方形水塊開始做起。在傳統的高度圖之中,水塊是由拆解成一條條直行橫列的長方形所組成,交會形成方形的元件群(圖五和圖六)。每一個元件本身都會分為兩個三角形。每一個三角形我們都會計算支撐它的平面的方程式,這能夠讓判斷某個點投影到上面時變得非常快速。
| 圖五:一個從下方往上看的4x4的水塊和水線(青色) |
圖六:一個從上往下看的5x5水塊和水線(青色)
在查詢某個點和水面的高度時,牽涉到要先找到某個點的投影會座落在哪個方形元件上—也就是支撐元件—接著要找到投影是在這個元件中哪兩個三角形上—也就是支撐三角形—。如果網格是對照著軸線的話,那麼找到支撐元件會是相當地快速。假設我們要找到點 的支撐元件。指定網格最左下角的點
的支撐元件。指定網格最左下角的點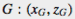 ,那麼該支撐元件的橫列指標 i 和直行指標 j 則為:
,那麼該支撐元件的橫列指標 i 和直行指標 j 則為:
其中 n 是橫列的數量(以及直行的數量)。現在我要引進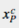 和
和 ,我稱它們為"元件內座標":
,我稱它們為"元件內座標":
其中 a 是每個元件的邊長。我選擇將每個元件三角化為右下和左上兩個三角形。如此一來,若 的話,那麼某個點的投影就會在右下這個三角形上,反之則是左上這個三角形。
的話,那麼某個點的投影就會在右下這個三角形上,反之則是左上這個三角形。
當我們知道是投影在哪個三角形上之後,若我們使用由三角形所定義之平面的方程式的話,我們就可以很快地判斷這個點在三角形之上或之下的高度為何。事實上,這個演算法在用來計算船殼頂點距離水面的高度時早就己經預先計算了所有三角形元件的平面方程式。
以點A,B, 和C所定義的平面上所有的點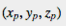 會符合:
會符合:
還有
以及
當有了平面的方程式後,我們就可以找出任意一個座標(x, y, z)的高度了:
裁剪用的演算法
當一個三角形的某些頂點在水面下而有些在水面上時,我們需要將三角形裁剪成一部份完全在水面上,以及另一部份完全在水面下。有個方法可以很簡易地進行裁剪,這方法既快速且能連續不間斷地動作。說到"連續不間斷地動作",我的意思是我們希望避免掉當頂點的高度有細微變化時,引起沉入部份瞬間大變動的狀況。如果我們很精確地將三角形裁成水面上下兩部份的話這個狀況就不會發生,這狀況的原因是近似法所導致的,而我們需要找出一個能運作良好的方法。這個問題在早先讓我感到挫折,而且有時候會導致浮力的不穩定,讓物體可能會很明顯地突然跳起或沉入,讓整體的效果毀於一旦。
以下是我如何去決定怎麼裁剪部份沉入三角形的方法。每個頂點的高度都利用上述的水塊來計算。三個頂點照在水面上方的高度來向下排序,從最上面的到最深入水底的,並且以H, M, 和L來代表對比水平面來說最高,中間,和最低的點。我們將這些點的高度分別定為 ,
, ,和
,和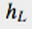 。
。
我們首先考慮H是在水面上而M和L是在水面下的案例(圖七)。所以:
| 圖七:當只有一個頂點在水面外的簡化版三角形剪裁。請注意我所選定的交會點 |
我假設水在點 和HM邊交會以及在點
和HM邊交會以及在點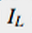 和HL邊交會,然後我假設ML邊是完全沉入在水底。這是剪裁演算法的簡化版本。交會點是座落於它們交叉的邊線附近,所以我們可以將它們的位置參數化:
和HL邊交會,然後我假設ML邊是完全沉入在水底。這是剪裁演算法的簡化版本。交會點是座落於它們交叉的邊線附近,所以我們可以將它們的位置參數化:
我用水面上方的高度來找適合這些參數的值:
下一步,我要研究H和M是在水上但L還是在水裡的案例(圖八)。和第一個案例類似,我們分別將 和
和 定為LM及LH和水的交會點。
定為LM及LH和水的交會點。
| 圖八:當有兩個頂點在水面外的簡化版三角形剪裁。 |
以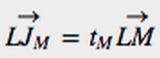 和
和 的位置
的位置
我們就用
| 圖九:這個範例就是裁剪是何時及如何會出錯的。這裡的兩個交會點應該和L有相等的距離,但是水平面在交會點之後突然地往下掉。裁剪演算法會將交會點 |
這個將問題簡化的方法的一大好處,除了是個快捷的方法外,就是每個邊線都會以獨特的方式來剪裁,不論座落於哪個三角形上。所以水線會不間斷地橫跨過三角形。此外,這個行為在三角形從第一個案例(只有H在水面上)轉移到第二個案例(H和M都在水面上)時也是不間斷的,因為在兩個案例中當M恰好在水面時交會點就會在水面。
計算靜壓力
當裁剪演算法在物件網格上所有的三角形都運行過後,我們就會得到一張列表列出有哪些是完全沉體三角形。作用在物體上的浮力是所有作用在完全沉體三角形靜壓力的總合。至於線性力,我們可以只加總靜壓力垂直方向的分力就好,因為我們已經證明其他的力會互相抵消了。沉體三角形的力可以表現為:
其中 是三角形中心在水裡的深度,而
是三角形中心在水裡的深度,而 是三角形指向外的法線。我們只需要再次使用水塊法就可以求得深度值。請注意,因為我們簡化裁剪的方式,有可能會導致沉體三角形的中心會在水塊之上。若是這樣,不去施加任何力在這個三角形上通常是不會有問題的,但很重要的是要抓出這個特定的案例,否則一個指向船體容積外部的力會被施加在這個面上。
是三角形指向外的法線。我們只需要再次使用水塊法就可以求得深度值。請注意,因為我們簡化裁剪的方式,有可能會導致沉體三角形的中心會在水塊之上。若是這樣,不去施加任何力在這個三角形上通常是不會有問題的,但很重要的是要抓出這個特定的案例,否則一個指向船體容積外部的力會被施加在這個面上。
記住,將靜壓力施加在三角形的中心而非真正的施力中心,就會造成被替代的容積中心附近產生殘餘力矩。若三角形的數量不多,而且不要有任何殘餘力矩這件事是很重要的話,那麼去計算三角形上的施力點就是必要的工作。附件A提供了在兩種底部為水平線的三角形型態上找出靜壓力施力中心的方法,也就是頂點朝上或下的三角形。一個任意的三角形沉體需要進一步地裁剪成兩個這樣的三角形,然後兩組的靜壓力和施力中心才能被計算並加總。
將以上拼湊起來
圖十列出了這個演算法的概觀。
| 圖十:演算法的概要 |
所以我們可以總結演算法的結構為以下(我假設x/z面是水平面,而y軸是垂直面)
- 在模擬時的每個步驟中,我會更新水塊的位置以跟上浮體。水塊不會很滑順地跟著載具,如同你在圖十一的gif檔所見。當船水平地移動時,它從原先的位置漂移的幅度夠大的話,水塊就會在一邊失去一個橫列(或直行)然後在另一邊添加一個列。當這個狀況發生時,水塊的座標(假設是西南那塊好了)會突然從上一動改變。
- 當我們判定了水塊的座標後,物體上網格的頂點就會取樣或計算與水面的高度。
- 對於那些如同傳統的高度圖那樣,因為水的高度而被往Y軸方向拉高的網格頂點上每個由兩個三角形組成的元件而言,我會計算因此產生的三角形所處的平面方程式。
- 我接著會藉由判定船殼上每個頂點是在哪個三角形上,並且用那個三角形的平面方程式來計算船殼上每個頂點在水面上的高度。
- 網格上每個三角形,既然已知每個頂點在水面上的高度,我會用裁剪演算法來產出有0, 1, 2 個在水裡的三角形。
- 我最後會反覆試驗這張三角形沉體列表來算出水中的力(靜壓力和動壓力)
這其中當然有很多的最佳化流程。舉例來說,我們可以先將船殼上的頂點垂直投影,以找出到底是哪些三角形元件會牽涉其中,然後只計算那些三角形的平面方程式。
| 圖十一:船隻在完全平滑的水面上只受到靜壓力時的動態反應。若在裡面釣魚的話事情會變得很糟。很明顯地,阻力在現實生活扮演了很重要的角色。 |
結論
這篇文章展示了一個將任意的網格和水平面交會時,以及計算這個網格所組成物件之靜壓力的演算法。如果寫了一個只會這樣運作的程式,那你就會得到一個像是在彈簧上不停上下擺動的船。這艘船會從水中被推往空中,然後因為重力往下掉,再度沉入水中然後又被推向空中。要用來穏定這個系統的東西叫做緩衝。動壓力會是下一篇文章的主題,而且對於將這個系統減震上非常有效,就如同它們在現實身活中所扮演的角色一樣。但也是有可能用偷吃步的方式,僅利用動態中從各個方向而來,特別是垂直方向上以速度為基礎的強力緩衝,來達到如同我們方才所述的演算法所得出靜壓力的感覺。
備註:
註一(*):若在某個深度中的一個點因為某種因素它的壓力比同深度的其它點還要小的話,這些同深度鄰近點的水因為受到較大的壓力,而會非常快地流動到那個壓力較小的點並且重新建立該深度均勻的壓力。唯一阻止水從因為較深而有較高壓力的地方往上流動到深度較淺且壓力較低的東西叫做重力,它也是為何隨著深度增加壓力也會逐潮增加的原因。
註二(**):順帶一提,當這個理論在法國被傳授時,它當時被稱為奧斯特洛格拉德斯基公式(Ostrogradsky Theorem)。後來我發現它同時也被稱為高斯公式(Gauss Theorem)。我在想(半開玩笑)是因為法國人捨不得將太多的理論歸功於德國,而在有選擇的情況下寧願讓給俄羅斯人嗎。美國人比較務實並且單純地將之稱為散度定理(Divergence Theorem)來避開這項爭議。
附件A:三角形沉體的靜壓力
要計算任意三角形完全沉體的靜壓力和力矩的話,將三角形裁剪成兩個較小的三角形是個有效的方式,每個三角形都有個邊是完美的水平線。這樣做的理由是因為要計算有水平邊三角形的靜壓力實在是簡單太多了:它可以被裁切成(幾乎)一條條水平方向的長方形(譯註:見圖十二),而這長方形表面上的壓力在每一個地方都是一樣的。
圖12展示了這樣的三角形,它水平的邊線比頂點還要深,其中 是頂點在水裡的深度,a和b是底邊頂點距離垂直線z軸的距離,h是頂點到底邊的深度差距,而C是個目前還未知的靜壓力施力點。目標就是要找出C點的位置。C點是當三角形上所有的靜壓力互相抵消那一瞬間的特殊點。
是頂點在水裡的深度,a和b是底邊頂點距離垂直線z軸的距離,h是頂點到底邊的深度差距,而C是個目前還未知的靜壓力施力點。目標就是要找出C點的位置。C點是當三角形上所有的靜壓力互相抵消那一瞬間的特殊點。
所以下一步就是要加總所有和可能C點有關的力矩,而當這個總合為零的時候我們就會找到這個特殊點了。
我將三角形切成無限小的一條條長方形。我要去將這些長方形參數化,用的是從頂點為0到底邊為1的參數 t 。每一條長方形的中心對應 t 的值是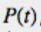 ,而
,而 是讓長方形的面積。在C附近的力矩是
是讓長方形的面積。在C附近的力矩是 和作用在長方形上的力
和作用在長方形上的力 的向量外積。
的向量外積。
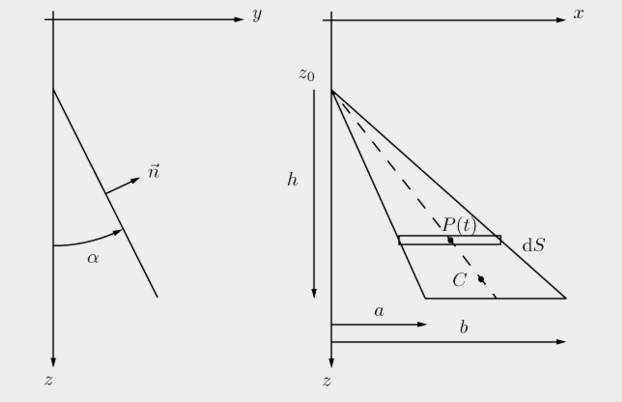 |
| 圖十二:有著水平底線的三角形。x軸和y軸被選定,所以三角形的法線位於(y, z)平上。x軸則和底邊平行。 |
當我們將長方形上的深度看成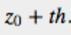 的話,長方形上的力就很容易計算了。
的話,長方形上的力就很容易計算了。
我們可以更進一步地將方程式展開,將 視為長方形的面積。它是高為
視為長方形的面積。它是高為 寬為
寬為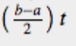 的長方形面積
的長方形面積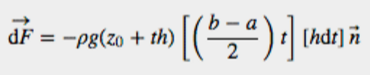
我們幾乎能夠展開 了。我們需要先表示
了。我們需要先表示 。請注意點C必須座落於三角形頂點和底線中間連線(也就是中線)的線上。這是因為在每個長方形上,中間點左方的力和右方的力是相等的,所以它們會在中點附近抵消掉。我們現在可以將點C和P以我們選定的x, y, 和z軸給展示出來。
。請注意點C必須座落於三角形頂點和底線中間連線(也就是中線)的線上。這是因為在每個長方形上,中間點左方的力和右方的力是相等的,所以它們會在中點附近抵消掉。我們現在可以將點C和P以我們選定的x, y, 和z軸給展示出來。
展開:
整合:
在這些之後我們可以求得尋求已久的方程式:
所以如果頂點剛好位於水面上的話會發生什麼事?這個點就會比三角形的中心,也就是高度往下算的2/3處(譯註:底邊往上1/3),還要來的低(譯註:從頂點算來3/4處)。
在另一方面,若深度為無限深的話,靜壓力的施力點確實會靠近三角形的中心點,越深的話就越近。
對於底邊朝上的三角來說,我會省下數學證明的時間。 的方程式就是:
的方程式就是:
再一次地,越深的話其點就會越靠近高度的2/3處(譯註:從底邊算來往下1/3處),但是在水平底邊在水面時該點會位於高度一半的地方。
參考文獻
1. Simship. Edouard Halbert.
2. "Buoyancy". Joel Feldman.
4. Simulating Ocean Water. Jerry Tessendorf.
5. Upper Bounds For Packing Of Spheres Of Several Radii. David De Laat, Fernando Mario De Oliveira Filho, Frank Vallentin.
翻譯:XDorz87
校訂:MilkReaver
沒有留言:
張貼留言